Pizza has become a new stable in dinner tables across the nation in the last few years. There is nothing easier than picking up the phone and ordering a fresh cheesy box. While ordering the delectable dish hardly requires brain power, the same cannot be said with cutting the pie into equal pieces. Surprisingly, scientists have taken up this dilemma in the light of circular geometry and have since formulated their own way to cut pizza perfectly.
What is dubbed to be the "Pizza Theorem" is a concept in elementary geometry that states "the equality of two areas that arise when one partitions a disk in a certain way." In terms of the actual, the theorem presupposes that should two people share a pizza, both would get an equal amount of the dish by slicing it a certain way. The first "Pizza study" was published almost half a century ago by the Mathematical Association of America.
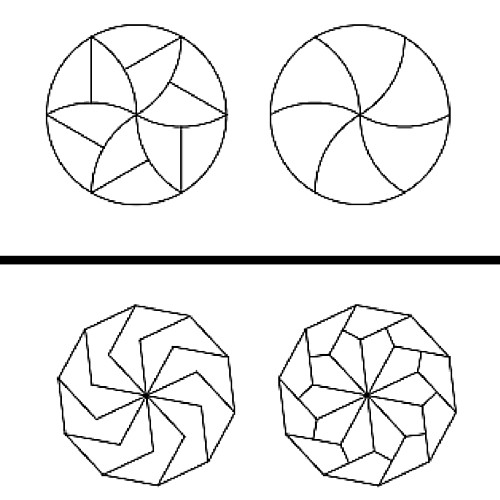
The diagram above illustrates the previous possible way a whole pizza can be sliced. According to earlier research, a disk which is pizza in this case can be divided in six slightly curved "shields." The six primary shields can subsequently be halved forming six more shields.
However according to a more recent study conducted by Joel Anthony Haddley and Stephen Worsley from the University of Liverpool, the initial "shields" can be taken a step further. On their paper published just last month, the pair presents the idea of creating partitions similar to the curved shields in earlier research albeit using straight lines with angles. Their research postulates that the pizza can be divided indefinitely by increasing the number of angles in each shield.
The new research is available for download here. A word of caution however - the study is not as easy as ordering pizza.



